快速入门¶

本章将介绍DS-PAW的各种功能的基本使用，具体包括： 结构弛豫计算 、 自洽计算 、 能带（投影能带）计算 、 态密度（投影态密度）计算 、 势函数计算 、 电子局域密度函数计算 ；在DS-PAW软件中大致的可以将参数分类几类：与物理结构相关的参数、与计算性质相关的参数、与计算精度相关的参数、与收敛相关的参数，这些参数中有很多都是有默认值的，且绝大多数参数不会影响计算结果；因此本章只设置了一些特别重要的参数，同时将对这些参数进行简单的讲解。

1.1 结构弛豫¶

在密度泛函理论（DFT）中结构弛豫指的改变初始的结构的晶胞及原子位置从而优化得到总能量的局域最小值。通过结构弛豫计算，可以减少在每个原子上的受力，从而得到较为稳定的结构（一定程度上，可以通过计算声子谱或者频率来验证结构的稳定性）。使用建模软件搭建的结构一般情况下原子受力都会比较大，且即使是其他DFT软件优化过的结构，在另外一个DFT计算软件中原子受力也不一定是最小的，因此一般情况下在计算某个结构的具体性质之前需要进行结构弛豫计算。

1.1.1 Si原子结构弛豫计算之准备输入文件¶

输入文件包含参数文件 relax.in 和结构文件 structure.as ， relax.in 如下：

# task type
task = relax
#system related
sys.structure = structure.as
sys.symmetry = false
sys.functional = LDA
sys.spin = none
#scf related
cal.methods = 2
cal.smearing = 1
cal.ksamping = G
cal.kpoints = [10, 10, 10]
#relax related
relax.max =  20
relax.freedom = atom
relax.convergence =  0.05
relax.methods = CG

relax.in 文件大致可以分为4部分参数：

第一部分指定计算类型，计算类型中只有task一个参数：

task ：设置计算类型，本次计算为relax结构弛豫；

第二部分指定系统相关参数，系统相关参数以sys.开头，一般是一些与体系的结构、泛函、磁性、对称性相关的参数：

sys.structure ：指定体系的结构文件，DS-PAW支持 .as 和 .json 的结构文件格式， .as 文件可以直接使用Device Studio软件生成，也可以自己手动生成；
sys.symmetry ：设置DS-PAW计算时是否需要使用对称性；
sys.functional ：设置泛函，目前程序支持 LDA 及 PBE 泛函；
sys.spin ：设置体系的磁性，由于 Si 没有磁性，因此将sys.spin设置为 none ；

第三部分指定计算相关的参数，这类参数以cal.开头：

cal.methods：设置自洽电子步优化方法，2表示使用 residual minimization 方法；
cal.smearing ：设置每个波函数的部分占有数方法，1表示使用 Gaussian smearing 方法；
cal.ksamping ：自动生成布里渊区 k点网格方法，G表示使用 Gamma centered 方法；
cal.kpoints ：设置布里渊区 k点网格取样大小，一般K点的大小需要根据体系晶格的大小和体系的周期性来设置，通常建议在具有周期性的方向上晶格矢量与K点的乘积不小于40，在不具有周期性的方向上将 K点设置为1即可；

第四部分指定结构弛豫相关参数，例如结构弛豫的方法、结构弛豫的类型、结构弛豫的精度等相关参数，结构弛豫指的是优化原子位置得到总能量的局域最小值的结构，一般也称之为离子步优化；

relax.max：设置结构驰豫时，最大的离子步步数；
relax.freedom ：设置结构驰豫的自由度，目前支持驰豫原子；
relax.convergence ：设置结构驰豫时，原子受力的收敛判据；
relax.methods ：设置结构驰豫的方法，目前支持 CG共轭梯度方法 ；

structure.as 文件参考如下：

Total number of atoms
2
Lattice
0.00 2.75 2.75
2.75 0.00 2.75
2.75 2.75 0.00
Direct
Si -0.115000000 -0.125000000 -0.125000000
Si 0.125000000 0.125000000 0.125000000

structure.as 文件结构固定，必须严格对照每一行写入相应信息:

第一行为固定提示行
第二行为总的原子个数
第三行为固定提示行
第四至六行为晶胞信息
第七行为原子坐标的形式，可选值为 Direct 和 Cartesian （全拼且首字母必须为大写）
第八行开始写入原子坐标信息，每一行的开头必须标注坐标所描述的原子的名称

由于本案例为结构弛豫计算，因此手动的将第一个 Si原子 的X坐标从 -0.125 改为 -0.115 ，这样能够更好的体现结构弛豫的效果。

1.1.2 程序运行¶

准备好输入文件之后，将 relax.in 和 structure.as 文件上传到安装了DS-PAW的环境上，这里将以linux环境为例子进行介绍；

在无图形界面的linux环境下运行软件的方式与在windows的环境下运行程序会有很大的区别，在linux下需要通过命令行的方式来运行程序；一般情况下需要先加在一下环境变量，通常会将需要用的环境变量写入文本或者 .bashrc ，通过 source 的命令来加载环境；环境加载完成之后，运行DS-PAW relax.in，此时使用的单机版的DS-PAW进行计算；如果运行 mpirun -np 6 DS-PAW relax.in ，此时使用的为并行版的DS-PAW进行计算。如果你需要使用排队系统（例如PBS、slurm等）提交任务，只要配置完成相应的 .pbs 或 .slurm 脚本，之后使用 qsub XXX.pbs或sbatch XXX.slurm 提交任务即可。

1.1.3 计算结果分析¶

根据上述的输入文件，计算完成之后将会得到 DS-PAW.log 、 relax.json 、 system.json 这3个文件:

DS-PAW.log ：DS-PAW计算之后得到的日志文件；
relax.json ：结构弛豫完成之后的结构文件，里面保存着每一个离子步完成之后的结构文件，可以将 relax.json 文件导入Device Studio软件中进行显示；生成的 relax.json 文件也可以直接用于之后自洽计算、能带、态密度等一系列计算中，只需在计算中将 sys.structure参数 指定当前 relax.json 文件即可；
system.json： system.json 文件中保存着最后一个离子步之后的计算结果，包含结构、磁矩、能量本征值、占据态、K点信息、原子受力、stress等相应的信息；

使用文本编辑器或者在线显示 json格式 的网页中打开 realx.json 文件，格式如下：

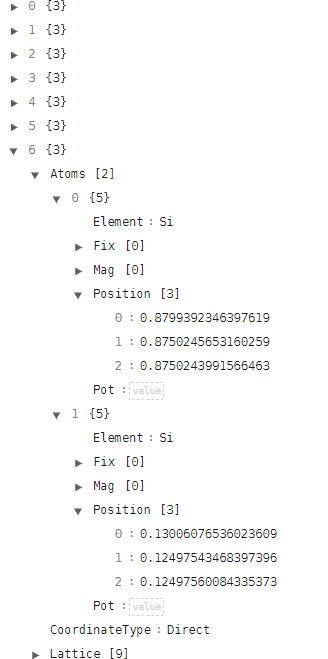
本次结构弛豫计算进行了6个离子步的计算，得到了6个结构文件，查看第6个结构可以发现两个原子的坐标都稍微有点变化，整体上两个原子之间的距离比手动移动原子之后的结构跟接近真实的坐标。在 system.json 文件中，查看 ForceOnAtoms 这个量，此时每个原子上的受力如下：

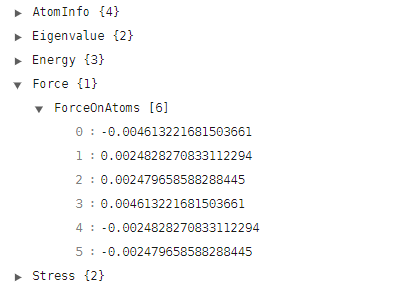
注解

DS-PAW运行命令为软件名+输入文件名，如果你的输入文件名为abc.in那么只要执行DS-PAW abc.in即可。

1.2 自洽计算¶

自洽计算能够得到特定晶体的电荷密度和波函数，有了电荷密度之后才能有计算该体系的能带、态密度等电子结构性质。特别需要注意是：自洽与能带、态密度等电子结构性质计算是有先后顺序的，必须先进行自洽计算得到电荷密度才能进一步计算能带、态密度等电子结构性质。

1.2.1 Si原子自洽计算之准备输入文件¶

输入文件包含参数文件 scf.in 和结构文件 structure.as ， scf.in 如下：

# task type
task = scf
#system related
sys.structure = structure.as
sys.symmetry = false
sys.functional = LDA
sys.spin = none
#scf related
cal.methods = 2
cal.smearing = 1
cal.ksamping = G
cal.kpoints = [10, 10, 10]
cal.cutoffFactor = 1.5
#outputs
io.charge = true
io.wave = true

scf.in 输入参数介绍：

可以看到 scf.in 的输入文件中很多参数与结构弛豫的参数名是一致的，其设置方法也是一致的，这里只着重介绍一些前面没设置过或设置有些不同的参数：

task ：本次计算为 scf 自洽计算，因此将task设置为 scf ；
cal.cutoffFactor ：表示截断能参数 cal.cutoff 的系数，在DS-PAW程序中，如果 cal.cutoff 参数缺失，程序将根据元素的截断能设置默认的平面波截断， cal.cutoffFactor 参数就是在 cal.cutoff 上设置乘以一个系数；
io.charge ：当io.charge设置为 true 时，表示计算完成之后输出电荷密度的二进制文件rho.bin和json文件rho.json，二进制rho.bin文件用于后续的后处理计算，例如能带、态密度等，rho.json文件用于显示；
io.wave ：当io.wave设置为 true 时，表示计算完成之后输出波函数的二进制文件wave.bin，用户可以在后续的后处理计算中选择是否使用wave.bin开始计算；

structure.as 文件参考如下：

Total number of atoms
2
Lattice
0.00 2.75 2.75
2.75 0.00 2.75
2.75 2.75 0.00
Direct
Si -0.125000000 -0.125000000 -0.125000000
Si 0.125000000 0.125000000 0.125000000

由于本案例为自洽计算只是为了计算得到特定体系的电子结构，因此不需要手动改变原子位置；

注解

io类参数只在结构弛豫和自洽中起作用，例如io.charge在其他计算情况下将不会生成rho.bin或rho.json文件；
在结构弛豫和自洽中，还能够保存elf、potential的数据，只需要将io.elf和io.potential设置为true即可；
如果用户想要使用自己优化的结构，只需在计算中将sys.structure参数指定绝对路径或相对路径下的relax.json，也可以将relax.json文件复制到本次计算的目录中，设置sys.structure=./relax.json即可；
带自旋体系的计算案例详解第二章的NiO案例。

1.2.2 程序运行¶

准备好输入文件 scf.in 和 structure.as 之后，按照结构弛豫中介绍的方法执行 DS-PAW scf.in 。

1.2.3 计算结果分析¶

根据上述的输入文件，计算完成之后将会得到 DS-PAW.log 、 system.json 、 rho.bin 、 rho.json 、 wave.bin 这5个文件。

rho.bin ：电荷密度的二进制文件，用于后续的后处理计算；
rho.json ：电荷密度的 json 格式文件，用来显示电荷密度的结果；目前Device Studio软件中 rho.json 的数据显示还在开发中，因此使用python脚本将 rho.json 格式的转化成 VESTA 软件支持的格式，具体操作如下：

DS-PAW使用 pymatgen 的画图程序来显示的二维数据，使用 VESTA 来显示三维数据。注意：以下python脚本依赖于python环境、python Pymatgen库和Dspawpy库，详情参见辅助工具使用。

在计算目录中新建一个 trans_rho.py 文件，内容如下：

import json
from dspawpy.io import write_VESTA_format

with open("./rho.json","r") as file:
   rho = json.load(file)

write_VESTA_format(rho["AtomInfo"], [rho["Rho"]["TotalCharge"]], "DS-PAW-rho.vesta")

第1，2行为需要导入的 python 库函数；
第4，5行为需要读取的 json 文件；
第7行为执行 write_VESTA_format 函数，将数据保存为VESTA可识别的格式，其中 rho["AtomInfo"] 为读取 rho.json 中的晶格及坐标信息, [rho["Rho"]["TotalCharge"]] 为 rho.json 中总的电荷密度的三维数据, DS-PAW-rho.vesta 表示生成的 vesta 格式数据；

执行 python trans_rho.py ；
得到转换后的文件 DS-PAW-rho.vesta ，将其重命名为 CHGCAR.vasp 以便在 VESTA 显示；
将 CHGCAR.vasp 文件拖入VESTA中则可得到如下的电荷密度图

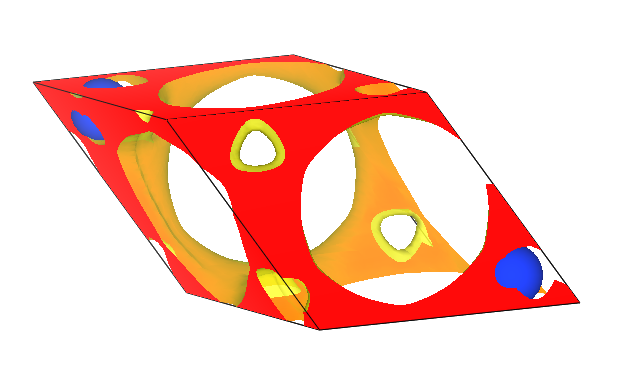
wave.bin ：波函数的二进制文件，用于后续计算；

1.3 能带计算¶

本节将从自洽出发介绍如何使用DS-PAW计算能带和投影能带。以Si体系为例进行自洽计算（见1.2节），自洽完成之后准备能带计算和投影能带计算，并对能带和投影能带作图分别进行分析。

1.3.1 Si能带输入文件¶

输入文件包含参数文件 band.in 、结构文件 structure.as 和上次自洽计算得到的二进制电荷密度文件 rho.bin ， band.in 如下：

# task type
task = band
#system related
sys.structure = structure.as
sys.symmetry = false
sys.functional = LDA
sys.spin = none
#scf related
cal.iniCharge = ./rho.bin
cal.methods = 2
cal.smearing = 1
cal.ksamping = G
cal.kpoints = [10, 10, 10]
cal.cutoffFactor = 1.5
#band related
band.kpointsLabel= [G,X,W,K,G,L]
band.kpointsCoord= [0, 0, 0, 0.5, 0, 0.5, 0.5, 0.25, 0.75, 0.375, 0.375, 0.75, 0, 0, 0, 0.5, 0.5, 0.5]
band.kpointsNumber= [30, 30, 30, 30, 30]

band.in 输入参数介绍：

在能带计算中可以尽量保留将 sys. 和 cal. 的参数到 band.in 中，之后设置能带计算特有的参数即可：

task ：本次计算为band能带计算，设置task为 band ；
cal.iniCharge ：表示读取电荷密度二进制文件，支持绝对路径及相对路径，这里./表示当前路径下的 rho.bin 文件；

能带计算中新增了一部分能带相关的参数，这些参数只在能带计算中起作用：

band.kpointsLabel ：表示能带计算时高对称点标签，一个 band.kpointsCoord 对应一个 band.kpointsLabel ；
band.kpointsCoord ：表示能带计算时高对此点的分数坐标，每三个数为一组；
band.kpointsNumber ：表示每相邻两个高对称点的间隔；

structure.as 文件同（见1.2节自洽计算 )。

注解

需要设置cal.iniCharge参数的时候，cal.cutoffFactor和cal.cutoff参数必须和之前自洽计算的结果一致，不然读取rho.bin的时候会出现格点数据不匹配的问题
band.kpointsCoord、band.kpointsLabel和band.kpointsNumber三个参数的维度需要统一

1.3.2 程序运行¶

准备好输入文件 band.in 和 structure.as 以及 rho.bin 之后,按照结构弛豫中介绍的方法执行 DS-PAW band.in 。

1.3.3 计算结果分析¶

根据上述的输入文件，计算完成之后将会得到 DS-PAW.log 、 band.json 这2个文件。

band.json ：能带计算完成之后的 json 数据文件；此时能带的数据也将会被保存在 band.json 中，具体的数据结构详见数据结构解析部分，使用 python 进行数据处理，具体操作如下：

在计算目录中新建一个 bandplot.py 文件，内容如下：

from pymatgen.electronic_structure.plotter import BSPlotter
from dspawpy.io import get_band_data

band_data = get_band_data("./band.json")

bsp = BSPlotter(bs=band_data)
fig = bsp.get_plot()
fig.savefig("bandplot.png",img_format="png")
fig.show()

第1、2行为需要导入的 python 库函数，这里用到了pymatgen中的 BSPloter 库，以及 dspawpy.io 中的 get_band_data 函数；
第4行为读取 band.json 文件构造 band_data 这个结构体；
第6行为调用BSPloter处理 band_data 数据；
第7行为使用 bsp 下面的 get_plot 进行画图；
第8行为保存图片的名称和格式，将数据保存为png格式命名为 bandplot.png ；
第9行为显示图片，如果用户运行的环境无法直接显示图片，用户可以将第七行注释了，之后打开 bandplot.png 文件查看。

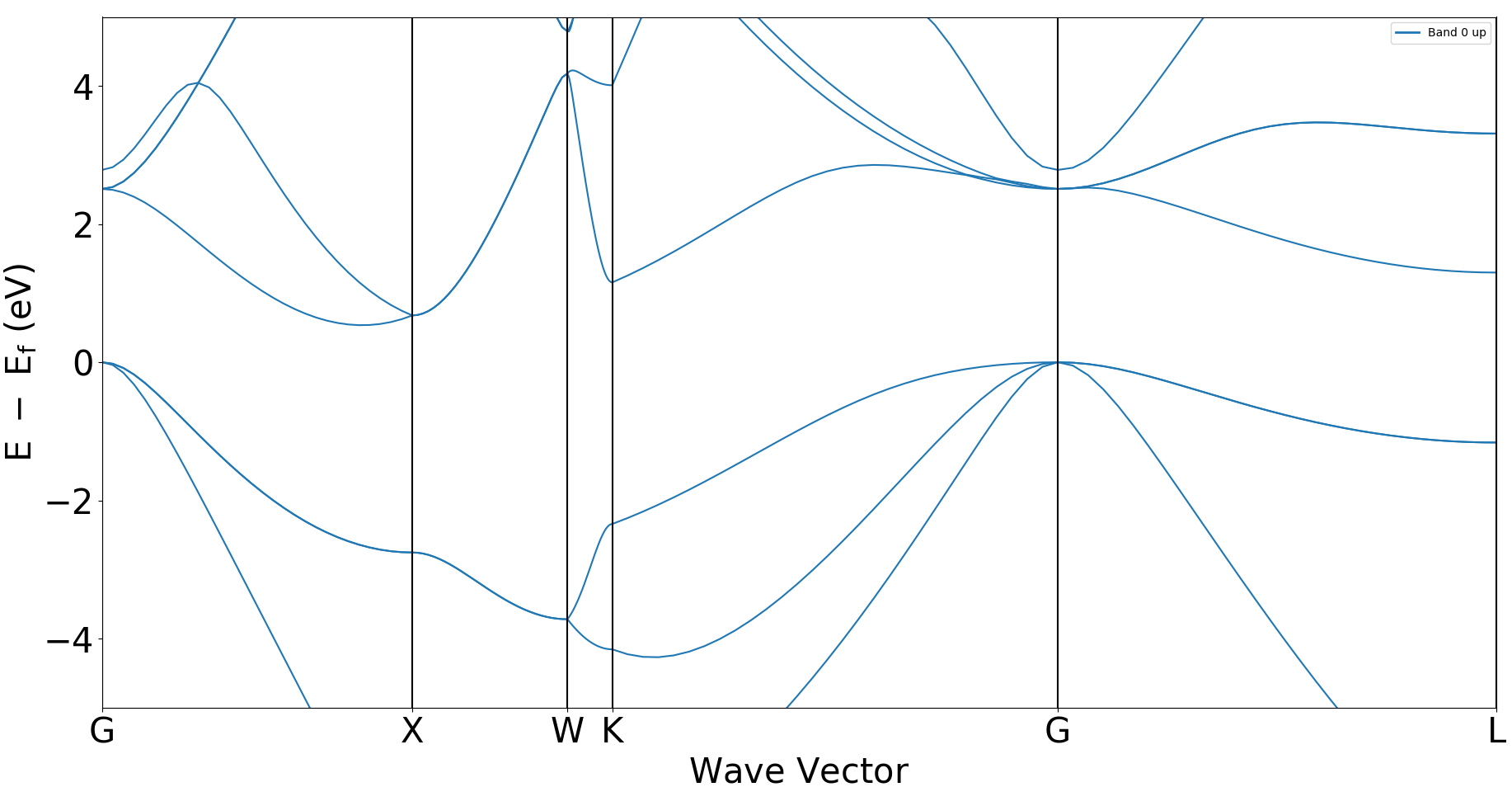
执行 python bandplot.py
生成 bandplot.png 文件

1.4 投影能带计算¶

投影能带是指在能带计算过程中将每条能带每个K点上的能量展开为每个原子及其轨道的贡献。

1.4.1 Si投影能带输入文件¶

投影能带的输入文件包含参数文件 pw_band.in 结构文件 structure.as 和上次自洽计算得到的二进制电荷密度文件 rho.bin ， pw_band.in 如下：

# task type
task = band
#system related
sys.structure = structure.as
sys.symmetry = false
sys.functional = LDA
sys.spin = none
#scf related
cal.iniCharge = ./rho.bin
cal.methods = 2
cal.smearing = 1
cal.ksamping = G
cal.kpoints = [10, 10, 10]
cal.cutoffFactor = 1.5
#band related
band.kpointsLabel= [G,X,W,K,G,L]
band.kpointsCoord= [0, 0, 0, 0.5, 0, 0.5, 0.5, 0.25, 0.75, 0.375, 0.375, 0.75, 0, 0, 0, 0.5, 0.5, 0.5]
band.kpointsNumber= [30, 30, 30, 30, 30]
band.project=true

pw_band.in 输入参数介绍：

pw_band.in 与普通能带的区别在于在计算参数中设置了 band.project 参数:

band.project ：表示在能带计算中打开能带投影的开关；

1.4.2 程序运行¶

准备好输入文件 pw_band.in 和 structure.as 以及 rho.bin 之后，按照结构弛豫中介绍的方法执行 DS-PAW pw_band.in 。

1.4.3 计算结果分析¶

根据上述的输入文件，计算完成之后将会得到 DS-PAW.log 、 band.json 这2个文件。

band.json ：能带计算完成之后的 json 数据文件；此时投影能带的数据也将会被保存在 band.json 中，具体的数据结构详见数据结构解析部分，使用 python 进行数据处理，具体操作如下：

在计算目录中新建一个 bandplot_projected.py 文件，内容如下：

from pymatgen.electronic_structure.plotter import BSPlotterProjected
from dspawpy.io import get_band_data

band_data = get_band_data("./band.json")
bsp = BSPlotterProjected(bs=band_data)
fig = bsp.get_projected_plots_dots({"Si":["p"]})

fig.savefig("bandplot_projected.png",img_format="png")
fig.show()

第1、2行为需要导入的 python 库函数，这里用到了pymatgen中的 BSPloter 库，以及:guilabel:dspawpy.io 中的 get_band_data 函数；
第4行为读取 band.json 文件构造 band_data 这个结构体；
第5行为调用BSPlotterProjected处理 band_data 数据；
第6行为使用 bsp 下面的 get_projected_plots_dots 进行画图,括号中 "Si":["p"] 表示画投影到p轨道的 Si 的能带，用户可以根据自己的体系和需要绘制的投影轨道对参数进行修改；
第8行为保存图片的名称和格式，这里将数据保存为png格式命名为 bandplot_projected.png ；
第9行为显示图片，如果用户运行的环境无法直接显示图片，用户可以将第七行注释了，之后打开 bandplot_projected.png 文件查看。

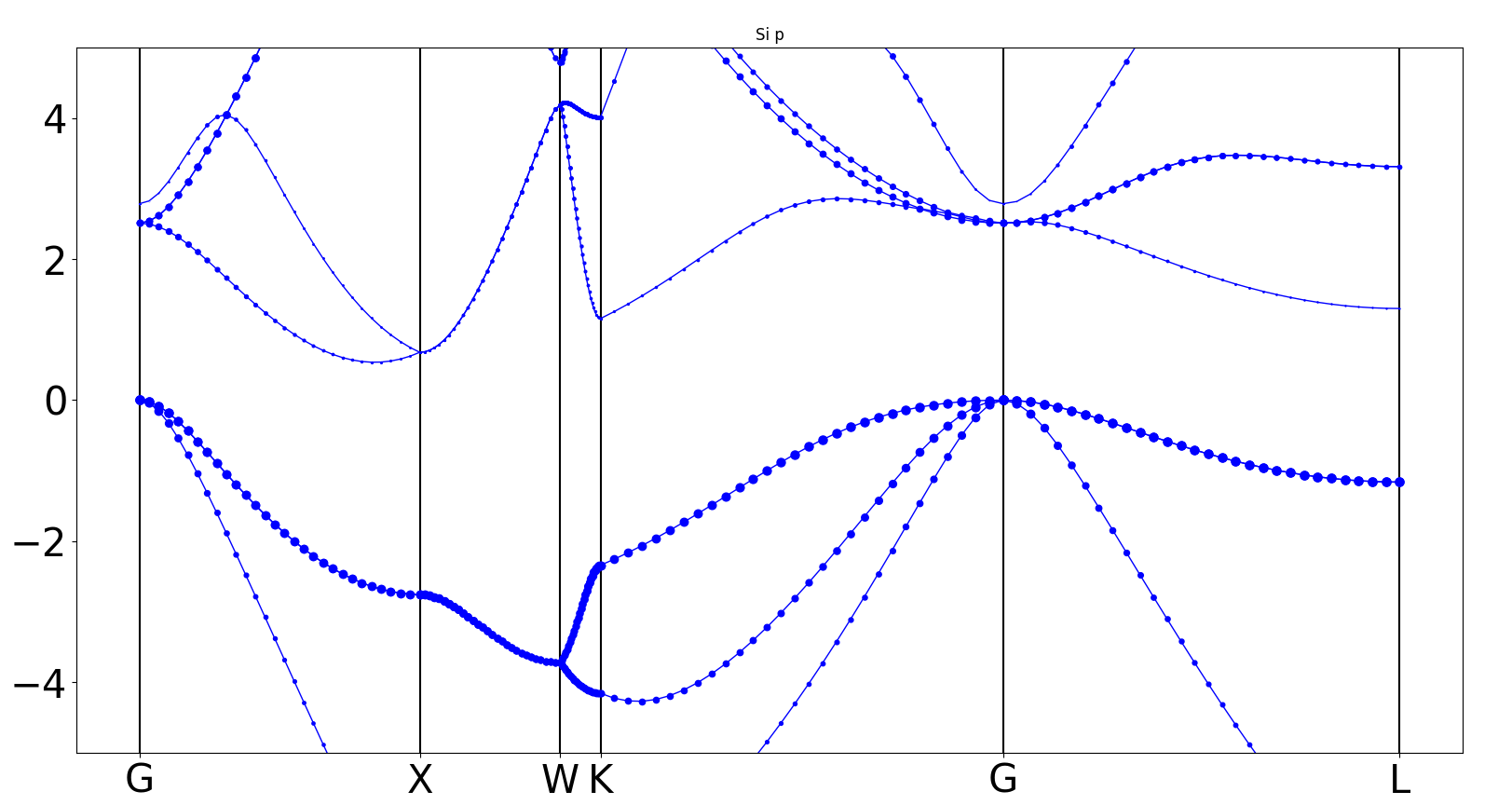
执行 python bandplot_projected.py ；
生成 bandplot_projected.png 文件

1.5 态密度计算¶

本节将从自洽出发介绍如何使用DS-PAW计算能带和投影能带。以Si体系为例进行自洽计算（见1.2节），自洽完成之后准备态密度计算和投影态密度能带计算，并对能带和投影能带作图分别进行分析。

1.5.1 Si态密度输入文件¶

输入文件包含参数文件 dos.in 结构文件 structure.as 和上次自洽计算得到的二进制电荷密度文件 rho.bin ， dos.in 如下：

# task type
task = dos
#system related
sys.structure = structure.as
sys.symmetry = false
sys.functional = LDA
sys.spin = none
dos.range=[-10, 10]
dos.resolution=0.05
dos.EfShift = true

#scf related
cal.iniCharge = ./rho.bin
cal.methods = 2
cal.smearing = 4
cal.ksamping = G
cal.kpoints = [20, 20, 20]
cal.cutoffFactor = 1.5
cal.sigma = 0.05
#dos related

#dos related
dos.range=[-10, 10]
dos.resolution=0.05
dos.EfShift = true

dos.in 输入参数介绍：

在态密度计算中可以尽量保留将 sys. 和 cal. 的参数到 dos.in 中，之后设置态密度计算特有的参数即可：

task ：本次计算为dos态密度计算，设置task为 dos ；
cal.iniCharge ：表示读取电荷密度二进制文件，支持绝对路径及相对路径，这里./表示当前路径下的 rho.bin 文件；
cal.kpoints ：为得到较为精确的态密度计算结果，需要设置更为密的 K 网格，因此需要重新设置 cal.kpoints ，一般该参数的取值为自洽时的两倍左右；
cal.sigma ：在态密度计算中为了得到比较精细的态密度，往往需要将 sigma 的值设置为尽可能的小；

态密度计算中新增了一部分态密度相关的参数，这些参数只在态密度计算中起作用：

dos.range ：态密度计算时能量的区间；
dos.resolution ：表示态密度计算能量间隔精度，态密度计算的点数即为 dos.range 的差值与 dos.resolution 的比值+1；
dos.EfShift ：当dos.EfShift为 true 时，表示将 dos.range 中设置的能量是相对于自洽费米能级的相对能量；

structure.as文件同（见1.2节）自洽计算的。

注解

需要设置cal.iniCharge参数的时候，cal.cutoffFactor和cal.cutoff参数必须和之前自洽计算的结果一致，不然读取rho.bin的时候会出现格点数据不匹配的问题。

1.5.2 程序运行¶

准备好输入文件 dos.in 和 structure.as 以及 rho.bin 之后，按照结构弛豫中介绍的方法执行 DS-PAW dos.in 。

1.5.3 计算结果分析¶

根据上述的输入文件，计算完成之后将会得到 DS-PAW.log 、 dos.json 这2个文件。

dos.json ：态密度计算完成之后的json数据文件；使用python进行数据处理，具体操作如下：

在计算目录中新建一个 dosplot_total.py 文件，内容如下：

from pymatgen.electronic_structure.plotter import DosPlotter
from dspawpy.io import get_dos_data

dos_data = get_dos_data("./dos.json")
dos_plotter = DosPlotter(stack=False,zero_at_efermi=True)
dos_plotter.add_dos('total dos',dos=dos_data)
dos_plotter.save_plot("dos_total.png",img_format="png")
dos_plotter.show()

第1、2行为需要导入的 python 库函数，这里用到了pymatgen中的 BSPloter 库，以及 dspawpy.io 中的 get_dos_data 函数；
第4行为读取 dos.json 文件构造 dos_data 这个结构体；
第5行为调用BSPlotterProjected处理 dos_data 数据，括号中 stack=False 表示态密度作图方式为曲线， stack=True 表示作图方式为面积， zero_at_efermi 控制是否将零点设为费米能级；
第6行使用 add_dos 来定义要处理的对象 dos ，调用前边定义好的dos对象 dos_data
第7行为保存图片的名称和格式，这里将数据保存为png格式命名为 dos_total.png ；
第8行为显示图片，如果用户运行的环境无法直接显示图片，用户可以将第七行注释了，之后打开 bdos_total.png 文件查看。

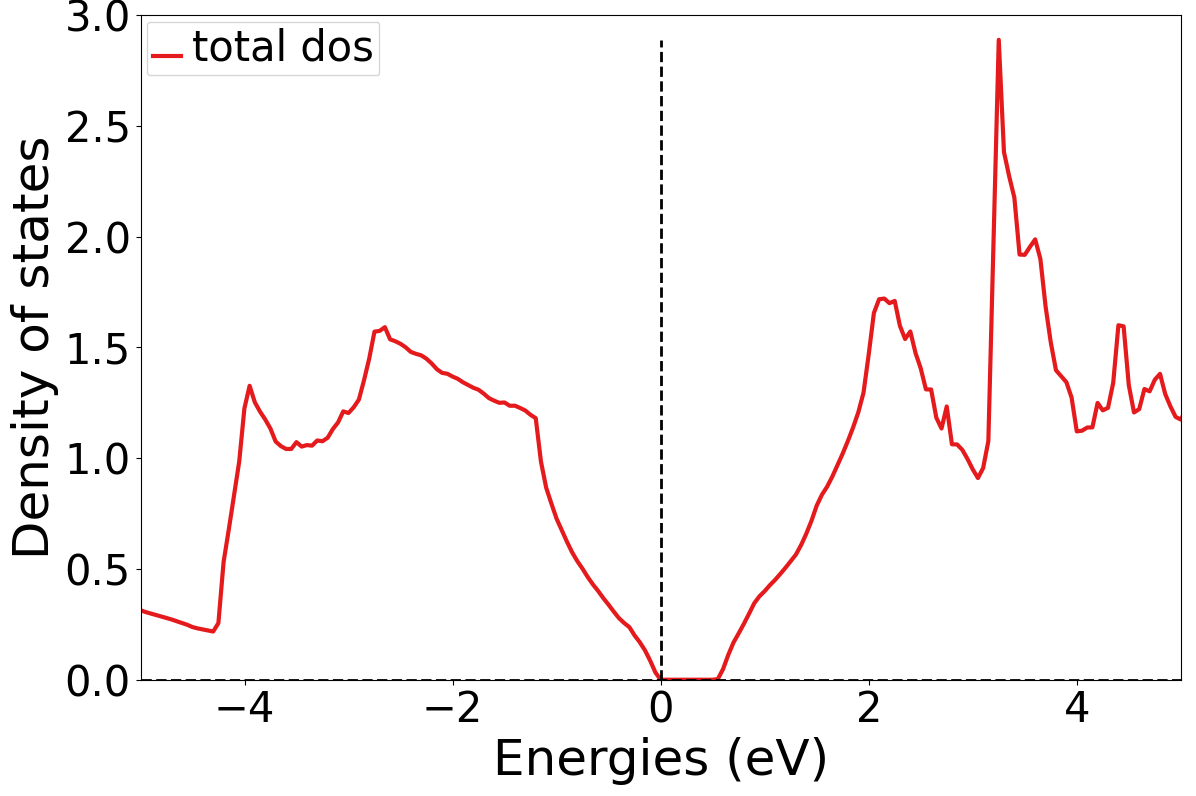
执行 python dosplot_total.py ；
生成 dos_total.png 文件

1.6 投影态密度计算¶

投影态密度的计算是指在态密度计算过程中将态每个能量下的态密度展开为每个原子及其轨道的态密度贡献。

1.6.1 Si投影态密度输入文件¶

投影态密度的输入文件包含参数文件 pdos.in 结构文件 structure.as 和上次自洽计算得到的二进制电荷密度文件 rho.bin ， pdos.in 如下：

# task type
task = dos
#system related
sys.structure = structure.as
sys.symmetry = false
sys.functional = LDA
sys.spin = none
#scf related
cal.iniCharge = ./rho.bin
cal.methods = 2
cal.smearing = 4
cal.ksamping = G
cal.kpoints = [20, 20, 20]
cal.cutoffFactor = 1.5
cal.sigma = 0.05
#dos related
dos.range=[-10, 10]
dos.resolution=0.05
dos.EfShift = true
dos.project = true

pdos.in 输入参数介绍：

pdos.in 与普通态密度的区别在于在计算参数中设置了 dos.project 参数：

dos.project ：表示在态密度计算中打开态密度投影的开关；

1.6.2 程序运行¶

准备好输入文件 pdos.in 和 structure.as 以及 rho.bin 之后，按照结构弛豫中介绍的方法执行 DS-PAW pdos.in 。

1.6.3 计算结果分析¶

根据上述的输入文件，计算完成之后将会得到 DS-PAW.log 、 dos.json 这2个文件。

dos.json ：态密度计算完成之后的 json 数据文件；此时投影态密度的数据也将会被保存在 dos.json 中，具体的数据结构详见数据结构解析部分，使用 python 进行数据处理，具体操作如下：

在计算目录中新建一个 dosplot_spd.py 文件，内容如下:

from pymatgen.electronic_structure.plotter import DosPlotter
from dspawpy.io import get_dos_data

dos_data = get_dos_data("./dos.json")
dos_plotter = DosPlotter(stack=False,zero_at_efermi=True)
dos_plotter.add_dos_dict(dos_data.get_spd_dos())
dos_plotter.save_plot("dos_spd.png",img_format="png")
dos_plotter.show()

第1、2行为需要导入的 python 库函数，这里用到了 pymatgen 中的 DosPlotter 库，以及 dspawpy.io 中的 get_dos_data 函数；
第4行为读取 dos.json 文件构造 dos_data 这个结构体；
第5行为调用BSPlotterProjected处理 dos_data 数据，括号中 stack=False 表示态密度作图方式为曲线， stack=True 表示作图方式为面积， zero_at_efermi 控制是否将零点设为费米能级；
第6行使用 add_dos_dict 获取投影信息，对 dos_data 进行 get_spd_dos 操作，获得投影到轨道的信息；
第7行为保存图片的名称和格式，这里将数据保存为png格式命名为 dos_spd.png ；
第8行为显示图片，如果用户运行的环境无法直接显示图片，用户可以将第七行注释了，之后打开 dos_spd.png 文件查看。

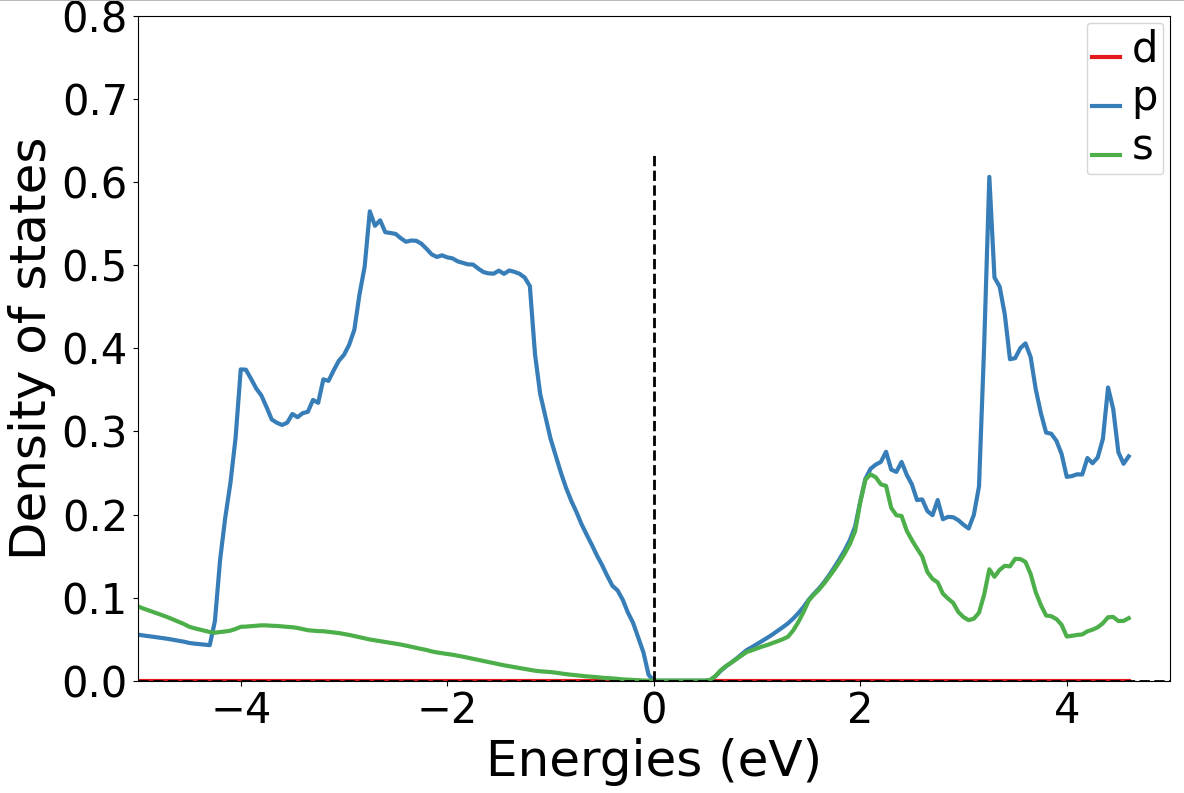
执行 python dosplot_spd.py ；
生成 dos_spd.png 文件

1.7 势函数计算¶

本节将从自洽出发介绍如何使用DS-PAW计算势函数。以 Si 体系为例进行自洽计算（见1.2节），自洽完成之后准备势函数输入文件，并对势函数的结果进行分析。

1.7.1 Si势函数输入文件¶

输入文件包含参数文件 potential.in 结构文件 structure.as 和上次自洽计算得到的二进制电荷密度文件 rho.bin ， potential.in 如下：

# task type
task = potential
#system related
sys.structure = structure.as
sys.symmetry = false
sys.functional = LDA
sys.spin = none
#scf related
cal.iniCharge = ./rho.bin
cal.methods = 2
cal.smearing = 1
cal.ksamping = G
cal.kpoints = [10, 10, 10]
cal.cutoffFactor = 1.5
#potential related
potential.type=all

potential.in 输入参数介绍：

在势函数计算中可以尽量保留将 sys. 和 cal. 的参数到 potential.in 中，之后设置势函数计算特有的参数即可：

task ：本次计算为 potential 势函数计算，设置task为 potential ；
cal.iniCharge ：表示读取电荷密度二进制文件，支持绝对路径及相对路径，这里./表示当前路径下的 rho.bin 文件；

势函数计算中新增了一个相关的参数：

potential.type ：表示保存势函数的类型，当选择 all 的时候，势函数计算完成之后将分别保存局域势函数和静电势函数；

structure.as 文件同（见1.2节）自洽计算的。

注解

需要设置cal.iniCharge参数的时候，cal.cutoffFactor和cal.cutoff参数必须和之前自洽计算的结果一致，不然读取rho.bin的时候会出现格点数据不匹配的问题；
本案例是调用自洽的结果进行势函数计算，用户也可以在task=scf时设置io.potential=true，此时也能保存potential.json文件。

1.7.2 程序运行¶

准备好输入文件 potential.in 和 structure.as 以及 rho.bin 之后，按照结构弛豫中介绍的方法执行 DS-PAW potential.in 。

1.7.3 计算结果分析¶

根据上述的输入文件，计算完成之后将会得到 DS-PAW.log 、 potential.json 这2个文件。

potential.json ：势函数计算完成之后的 json 数据文件；因此使用 python 脚本将 potential.json 格式的转化成 VESTA 软件支持的格式，具体操作如下：

在计算目录中新建一个 trans_potential.py 文件，内容如下：

import json
from dspawpy.io import write_VESTA_format

with open("./potential.json","r") as file:
   potential = json.load(file)

write_VESTA_format (potential["AtomInfo"], [potential["Potential"]["TotalElectrostaticPotential"], potential["Potential"]["TotalLocalPotential"]], "DS-PAW-potential.vesta")

第1，2行为需要导入的 python 库函数；
第4，5行为需要读取的 json 文件，这里 ./potential.json 指的时读取当前路径下的 potential.json ，如果需要读取其他的 json* 文件可以自行修改；
第7行为执行 write_VESTA_format 函数，将数据保存为 VESTA 可识别的格式，其中 potential["AtomInfo"] 为读取 potential.json 中的晶格及坐标信息, potential["Potential"]["TotalElectrostaticPotential"] 为 potential.json 中总的静电势的三维数据, "DS-PAW- potential.vesta" 表示将这些数据写入到 DS-PAW- potential.vesta 文件中；

执行 python trans_ potential.py ；
得到转换后的文件 DS-PAW- potential.vesta ，将其重命名为 potential.vasp 以便在 VESTA 显示；
将 potential.vasp 文件拖入 VESTA 中则可得到如下的势能图，展现的效果可以通过设置 vesta中Isosurface level 数值来调节，具体步骤为 vesta-properties-Isosurfaces-Isosurface level 。

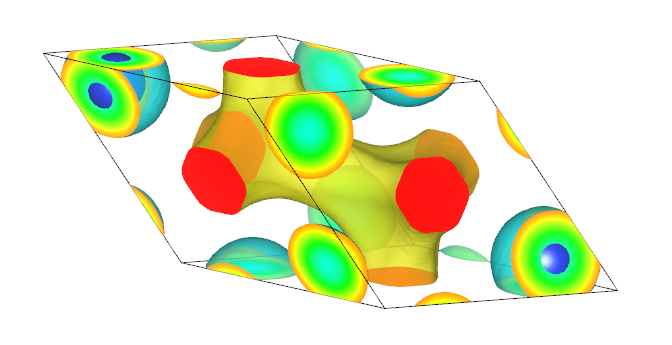
同时也可以将势函数处理得到面内平均图，具体操作如下：

在计算目录中新建一个 plot_potential_charge.py 文件，内容如下：

import json
import numpy as np
from dspawpy.plot import plot_potential_along_axis

with open("./potential.json","r") as file:
   potential = json.load(file)

grid = potential["AtomInfo"]["Grid"]
total_charge=np.asarray(potential["Potential"]["TotalLocalPotential"]).reshape(grid,order="F")

plt = plot_potential_along_axis(total_charge,axis=2,smooth=False)
plt.legend()
plt.show()

第1，2，3行为需要导入的 python 库函数，这里用到了 dspawpy.io 中的 plot_potential_along_axis 函数；
第5，6行为需要读取的 json 文件，这里 ./potential.json 指的时读取当前路径下的 potential.json ，如果需要读取其他的 json 文件可以自行修改；
第8行为执行grid函数，其中 potential["AtomInfo"]["Grid"] 为读取 potential.json 中的晶格及坐标信息;
第9行为执行 total_charge 函数，其中 potential["Potential"]["TotalLocalPotential"] 为读取 potential.json 中的局部势能信息,
第10行调用 plot_potential_along_axis 函数作图， smooth=False 则不作宏观平均图；
第11行为设置图例；
第12行为显示图片

执行 python plot_potential_charge.py ；

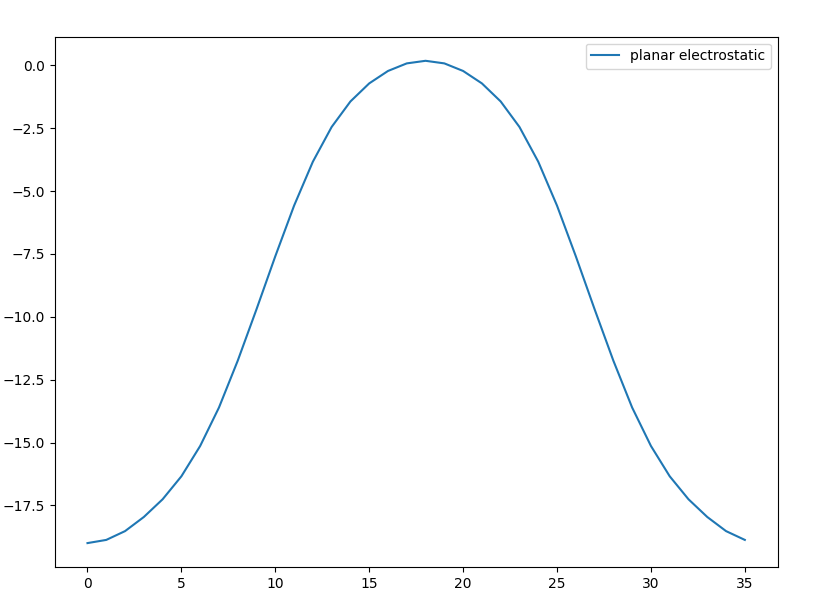
1.8 电子局域密度ELF计算¶

本节将从自洽出发介绍如何使用DS-PAW计算ELF。以Si体系为例进行自洽计算（见1.2节），自洽完成之后准备ELF计算，并对ELF作图进行分析。

1.8.1 Si ELF输入文件¶

输入文件包含参数文件 ELF.in 结构文件 structure.as 和上次自洽计算得到的二进制电荷密度文件 rho.bin ， ELF.in 如下：

# task type
task = elf
#system related
sys.structure = structure.as
sys.symmetry = false
sys.functional = LDA
sys.spin = none
#scf related
cal.iniCharge = ./rho.bin
cal.methods = 2
cal.smearing = 1
cal.ksamping = G
cal.kpoints = [10, 10, 10]
cal.cutoffFactor = 1.5

ELF.in 输入参数介绍：在ELF计算中可以尽量保留将 sys. 和 cal. 的参数到 ELF.in 中： task：本次计算为ELF计算，设置task为elf；

cal.iniCharge ：表示读取电荷密度二进制文件，支持绝对路径及相对路径，这里./表示当前路径下的 rho.bin 文件；

structure.as 文件同（见1.2节）自洽计算的。

注解

需要设置cal.iniCharge参数的时候，cal.cutoffFactor和cal.cutoff参数必须和之前自洽计算的结果一致，不然读取rho.bin的时候会出现格点数据不匹配的问题；
本案例是调用自洽的结果进行ELF计算，用户也可以在task=scf时设置io.elf=true，此时也能保存elf.json文件。

1.8.2 程序运行¶

准备好输入文件之后，将 ELF.in 和 structure.as 以及 rho.bin 文件上传到服务器上运行，按照结构弛豫中介绍的方法执行 DS-PAW ELF.in 。

1.8.3 计算结果分析¶

根据上述的输入文件，计算完成之后将会得到 DS-PAW.log 、 elf.json 这2个文件。

elf.json ：ELF计算完成之后的 json 数据文件；因此使用 python 脚本将 rho.json 格式的转化成 VESTA 软件支持的格式，具体操作如下：

在计算目录中新建一个 trans_elf.py 文件，内容如下：

import json
from dspawpy.io import write_VESTA_format

with open("./elf.json","r") as file:
   elf = json.load(file)

write_VESTA_format (elf ["AtomInfo"], [elf ["ELF"]["TotalELF"]], "DS-PAW-elf.vesta")

第1，2行为需要导入的 python 库函数
第4，5行为需要读取的 json 文件，这里 ./elf.json 指的时读取当前路径下的 elf.json ，如果需要读取其他的 json 文件可以自行修改；
第7行为执行 write_VESTA_format 函数，将数据保存为 VESTA 可识别的格式，其中 elf["AtomInfo"] 为读取 elf.json 中的晶格及坐标信息， elf ["ELF"]["TotalELF"] 为 elf.json 中总的局域电荷密度的三维数据,

DS-PAW- elf.vesta 表示将这些数据写入到 DS-PAW- elf.vesta 文件中；

执行 python trans_ elf.py ；
得到转换后的文件 DS-PAW-elf.vesta ，将其重命名为 elf.vasp 以便在 VESTA 显示；
将 elf.vasp 文件拖入 VESTA 中则可得到如下的势能图，展现的效果可以通过设置vesta中 Isosurface level 数值来调节，具体步骤为 vesta-properties-Isosurfaces-Isosurface level 。